Rectangular Microstrip Patch Antenna Calculator
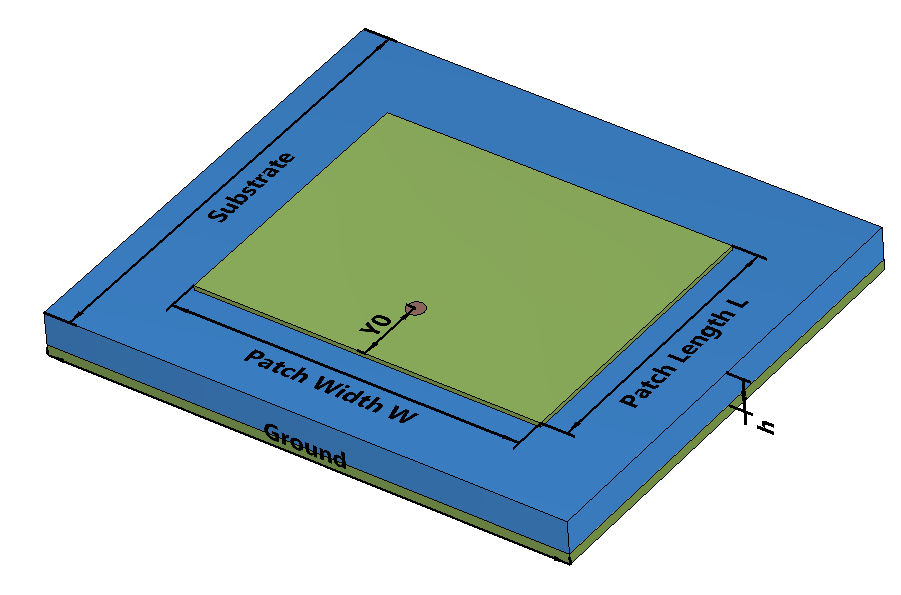
The dimensions of rectangular patch antenna is calculated for the lowest resonant frequency \(TM_{010} \)(dominant) mode. The ground plane is assumed to be infinite and all the metallic surfaces are lossless.
Formula
\(W = \frac{c}{2f_{r}}\sqrt{\frac{2}{\epsilon_{r}+1}}\)
\(L=\frac{c}{2f_{r}\sqrt{\epsilon_{reff}}}-0.824h \left( \frac{(\epsilon_{reff}+0.3)(\frac{W}{h}+0.264)}{(\epsilon_{reff}-0.258)(\frac{W}{h}+0.8)} \right)\)
\(\epsilon_{reff}=\frac{\epsilon_{r}+1}{2}+\frac{\epsilon_{r}-1}{2}\left [ \frac{1}{\sqrt{1+12\left (\frac{h}{W} \right )}}\right ]\)
\(G_{1}=\frac{1}{120\pi^2}\int_{0}^{\pi}\left [ \frac{sin\left ( \frac{K_{0}W}{2}cos\theta \right )}{cos\theta} \right ]^2sin^3\theta d\theta\)
\(G_{12}=\frac{1}{120\pi^{2} }\int_{0}^{\pi}\left [ \frac{sin\left ( \frac{K_{0}W}{2}cos\theta \right )}{cos\theta} \right ]^2J_{0}(K_{0}Lsin\theta)sin^3\theta d\theta\)
\(R_{in}(y=0)=\frac{1}{2(G_1+G_{12})}\)
\(R_{in}(y=y_0)=\frac{1}{2(G_1+G_{12})}cos^2(\frac{\pi}{L}y_0)\)
\(I_{1}=\int_{0}^{\pi}\int_{0}^{\pi}\left [\frac{sin\left ( \frac{K_{0}W}{2}cos\theta \right )}{cos\theta} \right ]^2 sin^3\theta cos^2( \frac{K_{0}L_e}{2}sin\theta sin\phi) d\theta d\phi\)
\(D=\left ( \frac{2\pi W}{\lambda_0} \right )^2\frac{\pi}{I_1}\)
| Where: |
| \(f_r \) = Resonant Frequency of Rectangular Patch Antenna |
| \(\epsilon_{r}\) = Substrate Relative Permittivity |
| \(h\) = Substrate Height |
| \(c \) = Velocity of Light |
| \(L \) = Physical Length of Patch |
| \(W \) = Physical Width of Patch |
| \(\epsilon_{reff} \) = Effective Relative Permittivity |
| \(K_{0}\) = Free-Space Phase Constant \(\frac{2\pi}{\lambda_0}\) |
| \(\lambda_0\) = Free-Space Wavelength |
| \(G_{1}\) = Single Slot Conductance |
| \(G_{12}\) = Mutual Conductance |
| \(R_{in}(y=0)\) = Input impedance of resonant patch at edge |
| \(R_{in}(y=y_0)\) = Input impedance of resonant patch at \(y=y_0\) |
| \(J_{0}\) = Bessel function of the first kind of order zero |
| \(D\) = Directivity of Patch Antenna |
Reference:
- [1] Balanis, C.A. (2016). Antenna Theory: Analysis and Design. 4th ed. Hoboken, New Jersey Wiley, pp.788–814. Chapter 14.2 Rectangular Patch.
Other Related Calculator:
-
Microstrip Circular Patch Antenna Calculator